Since the 1960s, mathematicians have used computers to help them discover patterns and formulate conjectures. In a recently published study , a team of researchers at the University of Sydney used artificial intelligence systems to try to solve some long-standing mathematical problems. In doing so, the researchers solved highly complex pure mathematics problems from the field of node theory and representation theory using AI developed by Google Deepmind.

The paper was written and presented by Alex Davies, Petar Veličković, Lars Buesing, Sam Blackwell, Daniel Zheng, Nenad Tomašev, Richard Tanburn, Peter Battaglia, Charles Blundell, András Juhász, Marc Lackenby, Geordie Williamson, Demis Hassabis and Pushmeet Kohli. This is the first time that machine learning has been used to prove new theorems, uncovering novel mathematical patterns and using these observations to guide intuition and propose conjectures, according to the researchers. These advances in mathematics have been made possible by the discovery of models used to formulate and prove useful conjectures that lead to theorems. Researchers work on computers, and machine learning is widely used in experimental mathematics, to generate and analyze complex data sets.

Geordie Williamson, a mathematician at the University of Sydney in Australia and co-author of the study said:

“Mathematical problems are widely regarded as some of the most intellectually challenging problems.”

The introduction of computers to generate data and test conjectures has allowed mathematicians to better understand problems that were previously inaccessible. Machine learning systems can search for patterns and scenarios for which they have not been coded: they take their training data and apply the same principles to new situations.

Geordie Williamson has used the power of DeepMind’s AI processes to explore conjectures in his area of specialty: representation theory, a branch that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces and also studies moduli over these abstract algebraic structures. Machine learning has thus made it possible to formulate conjectures and to suggest possible angles of attack to prove theorems, which was a first.

Discoveries that benefit several disciplines

Professor Geordie Williamson is Director of the Mathematical Research Institute at the University of Sydney and one of the world’s leading mathematicians. In 2018, he was elected the youngest living Fellow of the Royal Society in London, the oldest and one of the most prestigious scientific associations in the world. He is particularly interested in representation theory, a branch of mathematics that reduces problems in abstract algebra to problems in linear algebra – a more “accessible” and well-trained field.

Representation theory is ubiquitous in all fields of mathematics and has played an essential role and led to many generalizations. However, identifying new models is particularly complex. Professor Williamson explains:

“Working to prove or disprove long-held conjectures in my field involves dealing, at times, with infinite space and extremely complex sets of equations across multiple dimensions.”

Faced with the complexity of these conjectures, Professor Williamson decided to rely on Google Deepmind’s AI. He was desperate to prove the 40-year-old unsolved Kazhdan-Lusztig polynomial conjecture about deep symmetry in higher dimensional algebra.

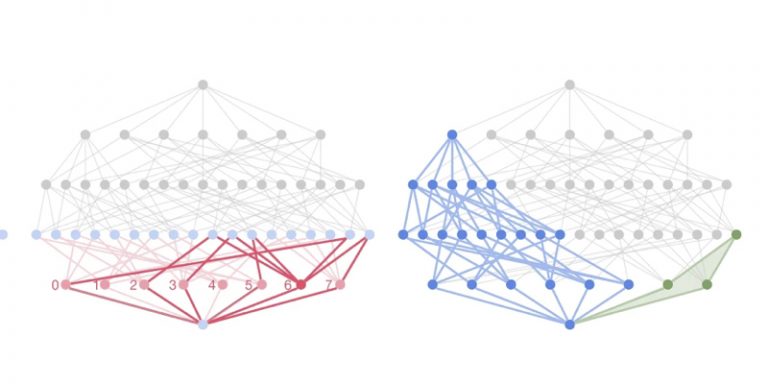
For this study, Professor Williamson collaborated with Professor Marc Lackeby and Professor András Juhász, both of Oxford University. They took the process a step further and discovered a new connection between algebraic and geometric invariants of knots, leading to a completely new theorem in mathematics.

In knot theory, invariants are used to solve the problem of distinguishing knots from each other; they also help mathematicians understand the properties of knots and their connection to other branches of mathematics. Knot theory also has many applications in other scientific disciplines; for example, it helps to understand DNA strands, fluid dynamics, and the interaction of forces in the sun’s corona. The discoveries made in mathematics through AI can therefore be used in many other areas of research.

Finding connections that the human mind does not always spot

The mathematician’s intuition plays an extremely important role in mathematical discovery, Professor Jushasz explains:

“Pure mathematicians work by formulating conjectures and proving them, which results in theorems.”

The framework shown in the figure below describes a general method by which mathematicians can use machine learning tools.

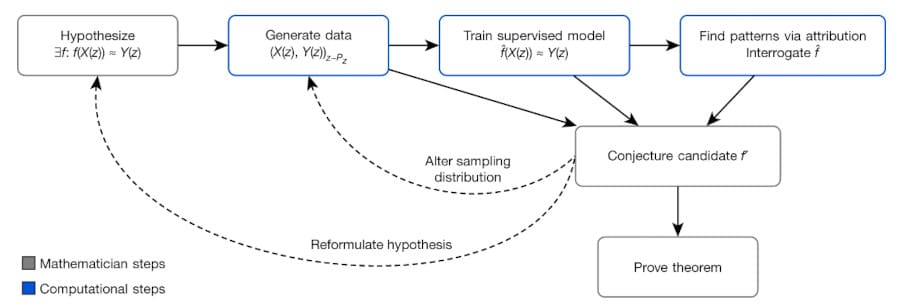
Machine learning has been able to make a difference by looking for novel patterns and scenarios, simply by applying principles from training data to new situations. Professor Jushasz states:

“We have shown that, when guided by mathematical intuition, machine learning provides a powerful Framework capable of discovering interesting and provable conjectures in domains where a large amount of data is available, or when objects are too large to be studied with conventional methods.”

The team has therefore proved that machine learning can be used in pure mathematics, to discover patterns and potential relationships between objects, new and unexpected connections between different areas of mathematics, which can be exploited to guide intuition towards new conjectures. Professor Lackeby said:

“I think the work we have done in Oxford and Sydney in collaboration with DeepMind demonstrates that machine learning can be a truly useful tool in mathematical research

.”
Professor Williamson added:

“Intuition can take us a long way, but AI can help us find connections that the human mind doesn’t always spot easily.”

Reference:
Davies, A., Veličković, P., Buesing, L. et al. Advancing mathematics by guiding human intuition with AI. Nature 600, 70-74 (2021). https://doi.org/10.1038/s41586-021-04086-x
DOI: https: //doi.org/10.1038/s41586-021-04086-x

Translated from Quand le machine learning permet le développement de modèles mathématiques inédits