In mathematics, a conjecture is a result that seems to be true, but for which no proof has been found: this is what makes it different from the theorem or property that can be proven in all cases where it is applicable. A Tel Aviv University postdoc specializing in machine learning (ML) and mathematics has developed an ML model that can search for counterexamples that can disprove conjectures with the help of his team of researchers. The system has already disproved five conjectures in the field of combinatorial analysis and graph theory.
Combinatorial analysis and graph theory
- Combinatorial or simply combinatorial analysis is a branch of mathematics that deals with the enumeration or counting of objects in different contexts. Thus, mathematicians study the set of combinations or configurations for a number of finite elements. For example, if we take several books, the objective of combinatorics is to know in how many different ways it will be possible to classify these books.
- Graph theory is a discipline of mathematics and computer science that studies graphs, an abstract model consisting of nodes (or vertices, points) connected by links (or edges, lines). Many theories of communication, networks (computer or social) exploit graphs to better understand their functioning.
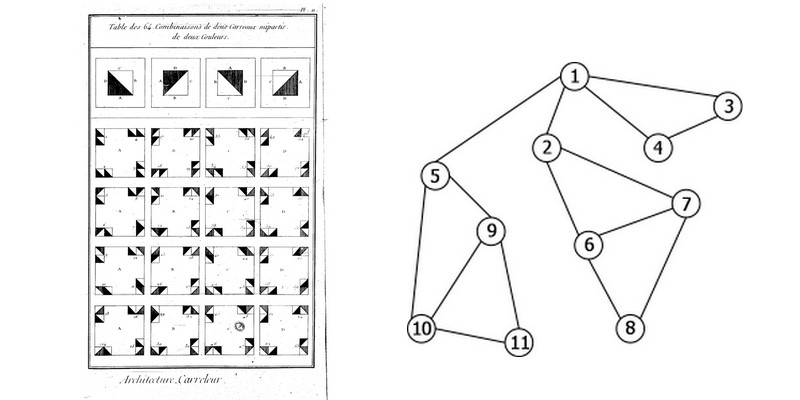
On the right, an arbitrary graph whose nodes are numbered.
Each of these two branches of mathematics has a large number of conjectures. These results are often considered to be accepted, because they work for many examples. However, if one of these examples does not work with this result, it is called a counterexample and thus disproves the conjecture.
A machine learning and reinforcement learning algorithm to disprove conjectures
For a conjecture to become a theorem, the result it evokes must be proven. On the other hand, to disprove a conjecture, it is enough to show that the result does not apply by taking an example for which the conjecture does not work, it is the famous counter-example. Adam Zsolt Wagner has developed a model of reinforcement learning based on this basic principle of mathematical proofs, the foundations of which he explains in an article.
The user proposes a conjecture and the algorithm proposes a measure that expresses the difficulty of disproving the proposition. The program creates random examples and uses these measures to evaluate their relevance as counterexamples, using machine learning. The AI eliminates the worst examples and replaces them with new randomly generated examples. The system repeats the process to find counterexamples that would refute a user’s suggestions.
For dozens of uses, the algorithm did not find an example that disproved these proposals. Five conjectures have been disproved, however, including one proposed by Richard Anthony Brualdi, a specialist in combinatorics and graph theory.
The rather strong opinions of mathematicians
Several mathematicians have expressed themselves on the quality of the model proposed by Adam Zsolt Wagner’s team. One of them is Leslie Hogben, from Iowa State University, whose conjecture was disproved by the AI:
“This is really impressive. What we’re seeing here is a huge benefit of artificial intelligence without a doubt, from a mathematical standpoint. It simply finds things for us, as a very perceptive person would. The counterexamples are needles in haystacks.”
Timothy Gowers of the Collège de France made a statement on Twitter around this AI model where he mentions some of what Adam Zsolt Wagner’s paper said while adding:
“This is an interesting proof of concept. Perhaps we can make it a simple conjecture testing tool that would be of great use to mathematical researchers.”
However, while Leslie Hogben is delighted that the model was able to disprove one of her conjectures , she believes that experts still need to be able to follow a computer proof:
“Personally, I would never have a problem with a computer disproof that can be verified. However, a computer proof that cannot be verified by hand would personally cause me some problems.”
In 1976, a theorem had been proved for the first time with the help of a computer: the computer had made an exhaustive list of all the examples for which the announced result was correct. Nevertheless, many mathematicians found the proof inelegant since it did not prove the conjecture in a classical way. In spite of this, information is nowadays widely used to solve mathematical problems.
Translated from Un modèle d’intelligence artificielle permet de réfuter certaines conjectures mathématiques