Dans de nombreux cas, lorsqu’il est question de systèmes complexes d’entités interagissant les unes avec les autres, les données sont structurées sous forme de graphe. Au cours des dernières années, l’application de méthodes d’apprentissage automatique à de telles données est devenue très courante, en particulier avec les réseaux de neurones graphiques (ou « réseaux GNN »).
La plupart du temps, on part du principe que le graphe est fixe dans les architectures GNN. Néanmoins, cette supposition est souvent trop simpliste. En effet, dans la mesure où le système sous-jacent de pléthore d’applications est dynamique, le graphe évolue au fil du temps. C’est par exemple la situation dans les réseaux sociaux ou les systèmes de recommandation, où les graphes décrivant l’interaction de l’utilisateur avec le contenu peuvent changer en temps réel. Plusieurs architectures GNN capables de traiter des graphes dynamiques, ont récemment été développées, y compris notre propre réseau
de graphes temporels (TGN) [1].
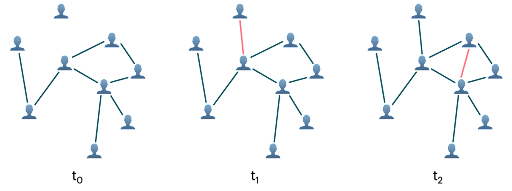
Dans cet article, nous nous intéressons à l’application de réseaux TGN à des graphes dynamiques de tailles variées, ainsi qu’à la complexité de calcul propre à ce type de modèles.
L’architecture TGN se caractérise par deux éléments principaux. Tout d’abord, des nœuds incorporés par le biais d’une architecture GNN classique, ici implémentée sous forme de réseau d’attention de graphes à couche unique [2]. Ensuite, une mémoire qui enregistre toutes les interactions passées de chaque nœud. Mise à jour à l’aide d’un réseau récurrent à porte (ou « réseau GRU ») lors de nouvelles interactions, il est possible d’y accéder en réalisant des opérations clairsemées de lecture/écriture [3].
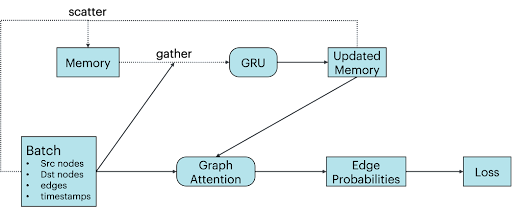
Nous nous concentrons sur les graphes qui évoluent au fil du temps via l’ajout de nouvelles arêtes. Ici, la mémoire d’un nœud contient des informations sur toutes les arêtes qui le ciblent, ainsi que sur leurs nœuds de destination respectifs. Par l’intermédiaire de contributions indirectes, la mémoire d’un nœud peut également contenir des informations sur des nœuds plus éloignés, ce qui rend les couches supplémentaires superflues dans le réseau d’attention de graphes.
Application à des graphes de petite taille
Nous avons débuté nos tests à l’aide de l’ensemble de données JODIE/Wikipédia [4], un graphe biparti représentant des articles Wikipédia et des utilisateurs et au sein duquel chaque arête entre un utilisateur et un article représente une modification apportée à l’article par l’utilisateur. Le graphe est constitué de 9 227 nœuds (8 227 utilisateurs et 1 000 articles) et de 157 474 arêtes avec horodatages. Les arêtes sont accompagnées de 172 vecteurs d’attributs LIWC dimensionnels [6] qui décrivent la modification. Au cours de la phase d’entraînement, les arêtes sont insérées lot par lot dans l’ensemble de nœuds initialement déconnecté, alors que le modèle est perfectionné via la perte contrastive d’arêtes réelles et d’arêtes négatives aléatoires. Les résultats de validation attestent de la probabilité d’identifier une arête réelle plutôt qu’une arête négative aléatoire.
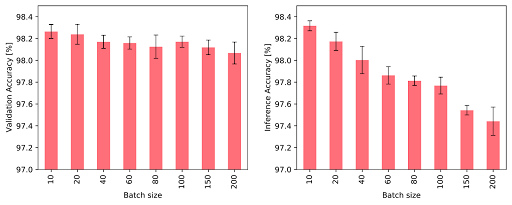
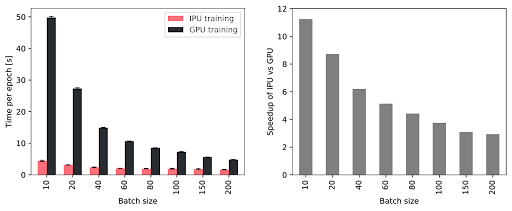
Logiquement, une taille de lot élevée a une incidence néfaste sur les phases d’entraînement et d’inférence : la mémoire des nœuds et la connectivité du graphe sont toutes deux mises à jour uniquement une fois que l’intégralité d’un lot a été traitée. Par conséquent, les événements ultérieurs au sein d’un lot peuvent être basés sur des informations obsolètes, les événements antérieurs n’étant pas pris en compte. Sur la Figure 3, nous constatons effectivement que des lots volumineux affectent négativement les performances. Cependant, l’emploi de lots de taille moindre exige un accès rapide à la mémoire, de sorte à bénéficier d’un débit élevé lors des phases d’entraînement et d’inférence. Avec un IPU profitant d’une importante quantité de mémoire intégrée, le débit devient supérieur à celui obtenu avec un GPU et des lots de plus petite taille (voir la Figure 4). Plus précisément, la phase d’entraînement du réseau TGN est 11 fois plus rapide avec une taille de lot de 10. À noter, d’ailleurs, que si la taille de lot passe à 200, la phase d’entraînement s’effectue toujours trois fois plus rapidement.
Étude des performances
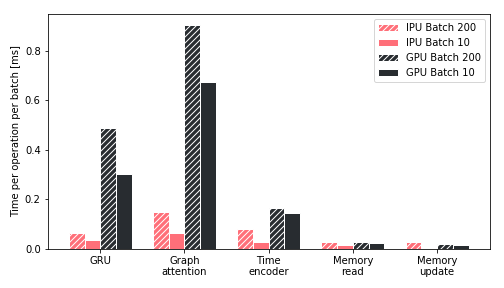
Pour mieux comprendre l’augmentation du débit lors de la phase d’entraînement sur un IPU, nous avons étudié la durée nécessaire à l’exécution des opérations clés induites par un réseau TGN sur différentes plateformes (voir la Figure 5). Nous avons observé que cette durée, avec un GPU, était dominée par le module d’attention et le réseau GRU, alors que les conditions sont plus favorables avec l’IPU. D’autre part, au cours de toutes les opérations, l’IPU gère les petites tailles de lot beaucoup plus efficacement, ce qui confirme les résultats illustrés par la prochaine figure. L’emploi de l’IPU est encore plus avantageux en cas d’opérations de moindre envergure et plus fragmentées au niveau de la mémoire. Globalement, nous pouvons affirmer que l’architecture de l’IPU est significativement plus performante que celle d’un GPU lorsque les opérations de calcul et les accès à la mémoire sont très hétérogènes.
Mise à l’échelle sur de larges graphes
Bien que la configuration par défaut du modèle TGN présente un « poids » relativement modeste avec environ 260 000 paramètres, la majeure partie de la mémoire intégrée est utilisée par la mémoire des nœuds si ce modèle est appliqué à de larges graphes. Toutefois, car les accès sont clairsemés, le tenseur ad hoc peut être réacheminé dans la mémoire hors puce, auquel cas l’utilisation de la mémoire intégrée ne dépend pas de la taille du graphe.
Pour tester l’architecture TGN avec de larges graphes, nous l’avons appliquée à un graphe anonymisé englobant 261 millions d’abonnements entre 15,5 millions d’utilisateurs de Twitter [7]. 728 horodatages différents, respectant un ordre temporel, sont assignés aux arêtes, mais ne fournissent aucune information sur la date réelle à laquelle des abonnements ont lieu. Car cet ensemble de données n’inclut aucun attribut de nœud ou d’arête, le modèle se base intégralement sur la topologie du graphe et l’évolution temporelle pour prédire de nouveaux liens.
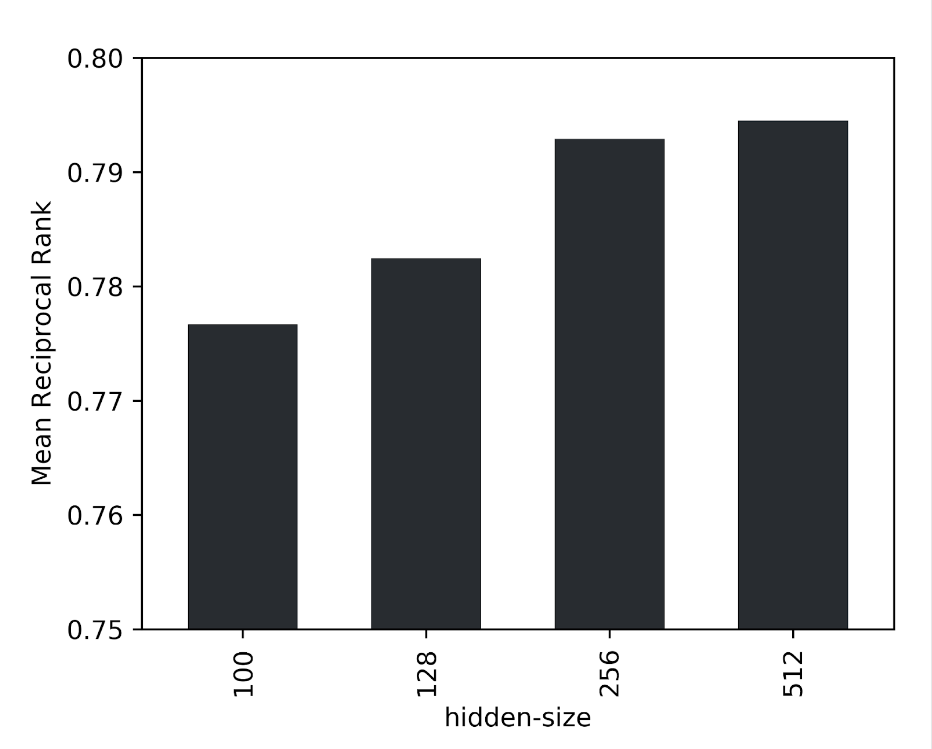
L’identification d’une arête positive en comparaison avec une seule arête négative étant trop simplifiée par la quantité élevée de données, nous avons opté, en tant que métrique de validation, pour le rang réciproque moyen de l’arête réelle parmi 1 000 arêtes négatives aléatoires. En outre, les performances du modèle se voient optimisées par une taille masquée plus large lors de l’augmentation de la taille de l’ensemble de données. Pour les données concernées, une taille latente de 256 constitue un bon compromis en termes de fiabilité et de débit.
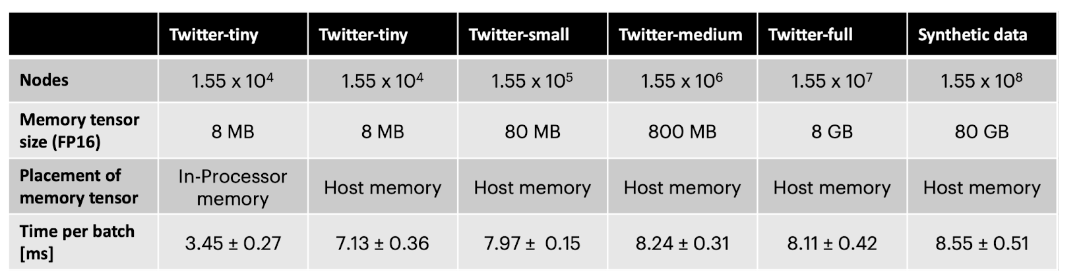
L’emploi de la mémoire hors puce par la mémoire des nœuds entraîne la réduction du débit de moitié environ. Cela étant dit, avec des graphes secondaires de tailles différentes, un ensemble de données synthétique comportant 10 fois plus de nœuds que le graphe Twitter et une connectivité aléatoire, le débit ne dépend quasiment pas de la taille du graphe (voir le Tableau ci-dessous). En adoptant cette technique, l’architecture TGN peut être appliquée à des tailles de graphes presque aléatoires, la seule limite étant la quantité de mémoire hôte disponible lorsque l’on cherche à bénéficier d’un débit très élevé au cours des phases d’entraînement et d’inférence.
Références :
[1] Rossi, E., Chamberlain, B., Frasca, F., Eynard, D., Monti, F. et Bronstein, M. Temporal graph networks for deep learning on dynamic graphs. arXiv preprint arXiv:2006.10637, 2020.
[2] https://towardsdatascience.com/temporal-graph-networks-ab8f327f2efe
[3] https://www.graphcore.ai/products
[4] Veličković, P., Cucurull, G., Casanova, A., Romero, A., Liò, P. et Bengio, Y. Graph Attention Networks. In International Conference on Learning Representations, 2018.
[5] Kumar, S., Zhang, X. et Leskovec, J. Predicting dynamic embedding trajectory in temporal interaction networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 1269 à 1278, 2019.
[6] Pennebaker, J. W., Francis, M. E. et Booth, R. J. Linguistic inquiry and word count: LIWC 2001. Mahwah : Lawrence Erlbaum Associates, 71(2001), 2001.
[7] El-Kishky, A., Markovich, T., Leung, K., Portman, F., Haghighi, A. et Xiao, Y. kNN-Embed: Locally Smoothed Embedding Mixtures For Multi-Interest Candidate Retrieval. arXiv preprint arXiv:2205.06205, 2022.