En mathématiques, une conjecture est un résultat qui semble vrai, mais pour lequel aucune démonstration n'a été trouvée : c'est ce qui la diffère du théorème ou de la propriété qui peut être prouvé dans tous les cas où elle est applicable. Un postdoctorant de l'Université de Tel-Aviv, spécialisé dans le machine learning (ML) et les mathématiques, a développé un modèle ML capable de chercher des contre-exemples pouvant réfuter des conjectures avec l'aide de son équipe de chercheurs. Le système a déjà contredit cinq conjectures dans le domaine de l'analyse combinatoire et de la théorie des graphes.
L'analyse combinatoire et la théorie des graphes
- L'analyse combinatoire ou simplement combinatoire est une branche qui s'intéresse au dénombrement ou au comptage des objets dans différents contextes. Ainsi, les mathématiciens étudient l'ensemble des combinaisons ou configurations pour un certain nombre d'éléments finis. Par exemple, prenons plusieurs livres, l'objectif de la combinatoire consiste à savoir de combien de manières différentes, il sera possible de classer ces livres.
- La théorie des graphes est une discipline des mathématiques et de l'informatique qui étudie les graphes, un modèle abstrait constitué de nœuds (ou sommets, points) reliés par des liens (ou arêtes, lignes). Nombreuses sont les théories de la communication, des réseaux (informatiques ou sociaux) qui exploitent les graphes afin de mieux comprendre leur fonctionnement.
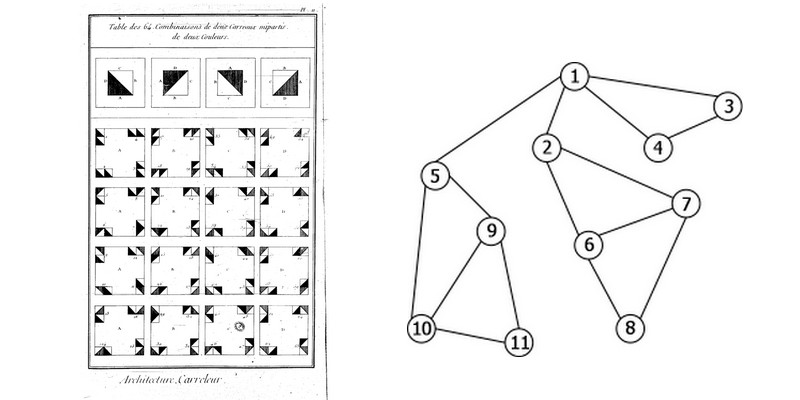 À gauche, une illustration de l'Encyclopédie de Diderot et D'Alembert proposant une partie des 64 combinaisons possibles pour placer du carrelage avec des carreaux mi-partis.
À gauche, une illustration de l'Encyclopédie de Diderot et D'Alembert proposant une partie des 64 combinaisons possibles pour placer du carrelage avec des carreaux mi-partis.À droite, un graphe quelconque dont les nœuds sont numérotés.[/caption]
Chacune de ces deux branches des mathématiques possède un grand nombre de conjectures. Ces résultats sont souvent considérés comme admis, car fonctionnant pour beaucoup d'exemples. Toutefois, si un de ces exemples ne fonctionne pas avec ce résultat, il est appelé contre-exemple et réfute donc la conjecture.
Un algorithme de machine learning et d'apprentissage par renforcement pour réfuter les conjectures
Pour qu'une conjecture devienne un théorème, il faut démontrer le résultat qu'il évoque. Par contre, pour réfuter une conjecture, il suffit de montrer que le résultat ne s'applique pas en prenant un exemple pour lequel la conjecture ne fonctionne pas, c'est le fameux contre-exemple. C'est en partant de ce principe basique des démonstrations mathématiques que Adam Zsolt Wagner a élaboré un modèle d'apprentissage par renforcement dont il explique les fondements dans un article.L'utilisateur propose une conjecture et l'algorithme propose une mesure qui exprime la difficulté à réfuter la proposition. Le programme crée des exemples aléatoirement et utilise ces mesures pour évaluer leur pertinence en tant que contre-exemple, grâce au machine learning. L'IA élimine les exemples les plus mauvais et les remplace par de nouveaux exemples générés aléatoirement. Le système réitère le processus afin de trouver des contre-exemples qui réfuteraient les propositions d'un utilisateur.
Pour des dizaines d'utilisations, l'algorithme n'a pas trouvé un exemple réfutant ces propositions. Cinq conjectures ont toutefois été réfutées : c'est le cas d'une conjecture proposée par Richard Anthony Brualdi, spécialiste en combinatoire et théorie des graphes.
Les avis plutôt tranchés des mathématiques
Plusieurs mathématiciens se sont exprimés sur la qualité du modèle proposé par l'équipe d' Adam Zsolt Wagner. On retrouve par exemple Leslie Hogben, de l’université d’État de l’Iowa, dont l’une des conjectures a été réfutée par l’IA :"C’est vraiment impressionnant. Ce que nous voyons ici est un énorme avantage de l’intelligence artificielle sans aucun doute, d’un point de vue mathématique. Elle trouve simplement des choses pour nous, comme le ferait une personne très perspicace. Les contre-exemples sont des aiguilles dans des bottes de foin."Timothy Gowers, du Collège de France, a fait une déclaration sur Twitter autour de ce modèle d'IA où il évoque certains propos de l'article d'Adam Zsolt Wagner tout en ajoutant :
"C'est une preuve de concept intéressante. Peut-être peut-on en faire un simple outil de vérification des conjectures qui serait d’une grande utilité pour les chercheurs en mathématiques."Toutefois, même si Leslie Hogben est ravie que le modèle ait pu réfuter une de ses conjectures , elle pense qu'il faut que les experts soient toujours en mesure de suivre une preuve informatique :
"Personnellement, je n’aurais jamais de problème avec une réfutation par ordinateur qui peut être vérifiée. Cependant, une preuve informatique qui n’est pas vérifiable à la main me poserait personnellement quelques problèmes."En 1976, un théorème avait été prouvé pour la première fois avec l'aide d'un ordinateur : celui-ci avait fait la liste exhaustive de l'ensemble des exemples pour lequel le résultat annoncé était correct. Néanmoins, de nombreux mathématiciens avaient trouvé la preuve inélégante puisqu'elle ne démontrait pas de manière classique la conjecture. Malgré cela, l'information est à l'heure actuelle énormément utilisée pour résoudre des problèmes mathématiques.