Depuis les années 1960, les mathématiciens ont utilisé des ordinateurs pour les aider à découvrir des modèles et à formuler des conjectures. Dans une étude récemment publiée, une équipe de chercheurs de l'Université de Sydney a utilisé des systèmes d'intelligence artificielle pour tenter de résoudre certains problèmes mathématiques de longue date. Les chercheurs ont ainsi résolu des problèmes de mathématiques pures, très complexes, du domaine de la théorie des noeuds et de la théorie des représentations grâce à l'IA développée par Google Deepmind.
L'article a été rédigé et présenté par Alex Davies, Petar Veličković, Lars Buesing, Sam Blackwell, Daniel Zheng, Nenad Tomašev, Richard Tanburn, Peter Battaglia, Charles Blundell, András Juhász, Marc Lackenby, Geordie Williamson, Demis Hassabis et Pushmeet Kohli. C’est, selon les chercheurs, la première fois que l’apprentissage automatique (ou machine learning) est mis à profit pour prouver de nouveaux théorèmes, mettant en évidence des modèles mathématiques inédits et utiliser ces observations pour guider l'intuition et proposer des conjectures. Ces progrès en mathématiques ont été rendus possible par la découverte de modèles utilisés pour formuler et prouver des conjectures utiles qui aboutissent à des théorèmes. Les chercheurs travaillent sur ordinateur, l’apprentissage automatique est d’ailleurs largement exploité en mathématiques expérimentales, pour générer et analyser des ensembles de données complexes.
Geordie Williamson, mathématicien à l’Université de Sydney en Australie et co-auteur de l’étude a déclaré :
"Les problèmes mathématiques sont largement considérés comme certains des problèmes les plus difficiles sur le plan intellectuel."L'introduction des ordinateurs pour générer des données et tester des conjectures a permis aux mathématiciens de mieux comprendre des problèmes qui étaient auparavant inaccessibles. Les systèmes d'apprentissage automatique peuvent rechercher des modèles et des scénarios pour lesquels ils n'ont pas été codés : ils prennent leurs données d'apprentissage et appliquent les mêmes principes à de nouvelles situations.
Geordie Williamson a utilisé la puissance des processus d’IA de DeepMind pour explorer des conjectures dans son domaine de spécialité : la théorie des représentations, une branche qui étudie les structures algébriques abstraites en représentant leurs éléments comme des transformations linéaires d’espaces vectoriels et qui étudie aussi les modules sur ces structures algébriques abstraites. Le machine learning a ainsi permis de formuler des conjectures et à suggérer des angles d’attaque possibles pour prouver des théorèmes, ce qui était une première.
Des découvertes qui profitent à plusieurs disciplines
Le professeur Geordie Williamson est directeur de l’Institut de recherche mathématique de l’Université de Sydney et l’un des plus grands mathématiciens du monde. En 2018, il a été élu le plus jeune membre vivant de la Royal Society de Londres, l’association scientifique la plus ancienne et l’une des plus prestigieuses au monde. Il s’intéresse tout particulièrement à la théorie des représentations, une branche des mathématiques qui permet de réduire des problèmes d’algèbre abstraite à des problèmes d’algèbre linéaire — un domaine plus "accessible » et mieux maîtrisé.Omniprésente dans tous les domaines des mathématiques, la théorie des représentations joue un rôle essentiel et a conduit à de nombreuses généralisations. Cependant, l’identification de nouveaux modèles est particulièrement complexe. Le professeur Williamson explique :
"Travailler pour prouver ou réfuter des conjectures de longue date dans mon domaine implique la prise en compte, parfois, d’un espace infini et d’ensembles d’équations extrêmement complexes à travers plusieurs dimensions".Devant la complexité de ces conjonctures, le professeur Williamson a décidé de s'appuyer sur l'IA de Google Deepmind. Il voulait à tout prix prouver la conjecture sur les polynômes de Kazhdan-Lusztig, non résolue depuis 40 ans, qui concerne la symétrie profonde dans l’algèbre de dimension supérieure.
Pour cette étude, le professeur Williamson a collaboré avec le professeur Marc Lackeby et le professeur András Juhász, tous deux membres de l’Université d’Oxford. Ces derniers, en poussant le processus un peu plus loin, ont découvert une nouvelle connexion entre les invariants algébriques et géométriques des nœuds, menant à un théorème complètement nouveau en mathématiques.
Dans la théorie des nœuds, les invariants sont utilisés pour résoudre le problème de la distinction des nœuds entre eux ; ils aident également les mathématiciens à comprendre les propriétés des nœuds et leur lien avec d’autres branches des mathématiques. La théorie des nœuds a également de nombreuses applications dans d’autres disciplines scientifiques ; elle aide par exemple à comprendre les brins d’ADN, la dynamique des fluides ou encore l’interaction des forces dans la couronne solaire. Les découvertes réalisées en mathématiques grâce à l’IA peuvent donc servir à de nombreux autres domaines de recherche.
Trouver des connexions que l’esprit humain ne repère pas toujours
L'intuition du mathématicien joue un rôle extrêmement important dans la découverte des mathématiques, le professeur Jushasz explique :"Les mathématiciens purs travaillent en formulant des conjectures et en les prouvant, ce qui aboutit à des théorèmes."Le framework illustré dans la figure ci-dessous décrit une méthode générale par laquelle les mathématiciens peuvent utiliser des outils d'apprentissage automatique.
[caption id="" align="alignnone" width="900"]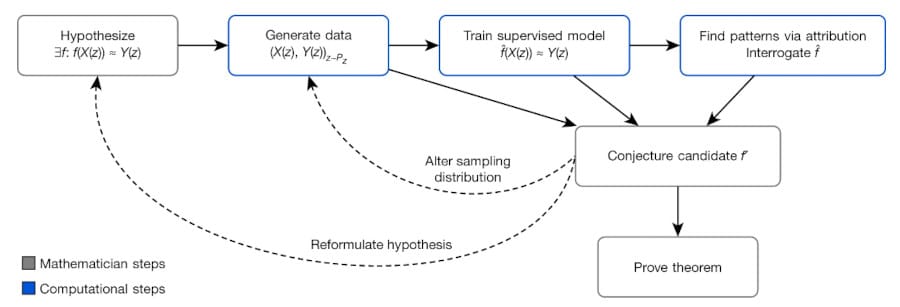 Le processus permet de guider l’intuition d’un mathématicien sur une fonction hypothétique f, en formant un modèle d’apprentissage automatique pour estimer cette fonction sur une distribution particulière de données PZ. Les enseignements tirés de la précision de la fonction apprise f^ et des techniques d’attribution qui lui sont appliquées peuvent aider à la compréhension du problème et à la construction d’une forme fermée f′. Le processus est itératif et interactif, plutôt qu’une seule série d’étapes. © A. Davies et al.[/caption]
Le processus permet de guider l’intuition d’un mathématicien sur une fonction hypothétique f, en formant un modèle d’apprentissage automatique pour estimer cette fonction sur une distribution particulière de données PZ. Les enseignements tirés de la précision de la fonction apprise f^ et des techniques d’attribution qui lui sont appliquées peuvent aider à la compréhension du problème et à la construction d’une forme fermée f′. Le processus est itératif et interactif, plutôt qu’une seule série d’étapes. © A. Davies et al.[/caption]
Le machine learning a pu faire la différence en recherchant des modèles et des scénarios inédits, simplement en appliquant les principes tirés des données d’entraînement à de nouvelles situations. Le professeur Jushasz affirme :
"Nous avons démontré que, lorsqu'il est guidé par l'intuition mathématique, l'apprentissage automatique fournit un Framework puissant capable de découvrir des conjectures intéressantes et prouvables dans des domaines où une grande quantité de données est disponible, ou lorsque les objets sont trop grands pour être étudiés avec des méthodes classiques."L’équipe a donc prouvé que l’apprentissage automatique peut être utilisé en mathématiques pures, pour découvrir des modèles et des relations potentielles entre les objets, des connexions nouvelles et inattendues entre différents domaines des mathématiques, qui peuvent être exploitées pour guider l’intuition vers de nouvelles conjectures. Le professeur Lackeby a déclaré :
"Je pense que le travail que nous avons réalisé à Oxford et à Sydney en collaboration avec DeepMind démontre que l’apprentissage automatique peut être un outil véritablement utile dans la recherche mathématique"Le professeur Williamson a ajouté :
"L’intuition peut nous mener loin, mais l’IA peut nous aider à trouver des connexions que l’esprit humain ne repère pas toujours facilement."Référence :
Davies, A., Veličković, P., Buesing, L. et al. Advancing mathematics by guiding human intuition with AI. Nature 600, 70–74 (2021). https://doi.org/10.1038/s41586-021-04086-x
DOI : https://doi.org/10.1038/s41586-021-04086-x


